Real Number

浮点数：不确定位数

Fixed-point representation

1. al overall number of bits is chosen

2. with a defined number of bits for the whole number part

3. and the remainder for the fractional part

• The binary point is set in a fixed position and it does not need to be stored in the memory

• Special attention needs to be paid to be position/ place values of those bits after the binary point

Floating point representation

1. The form:

   Mantissa x 2^exponent

2. examples

binary number to denary number:

Step1: 计算ex部分的二进制数，转换为十进制数。算出的十进制数为小数点位数n

Step2: mantissa的默认小数点位于左数第一数位和第二数位，将小数点向右移动n位

Step3: 小数点左侧为整数部分，即1,2,4,8…..，小数点右侧为小数部分：即2^1/2，2^1/4…..

Step4: 相加

Precision

Remember we have to decide:

1. the total number of bits used.

2. the number of bits used for matissa

3. the number of bits used for exponent.

Note:

1. 前后两个部分都是two’s compliment，前面表示整数部分，后面是exponential

2. mantissa表示精度，exponent表示范围，
   mantissa分到的数位越多，所表示的数字越精确；exponential的数位越多，所表示的数字范围越大
   

1. A binary representation is only an approximation of a real number.

2. Increasing the number of bits for mantissa gives a better precision

3. But leaves less number of bits for exponent, which reduces the range of numbers can be represented

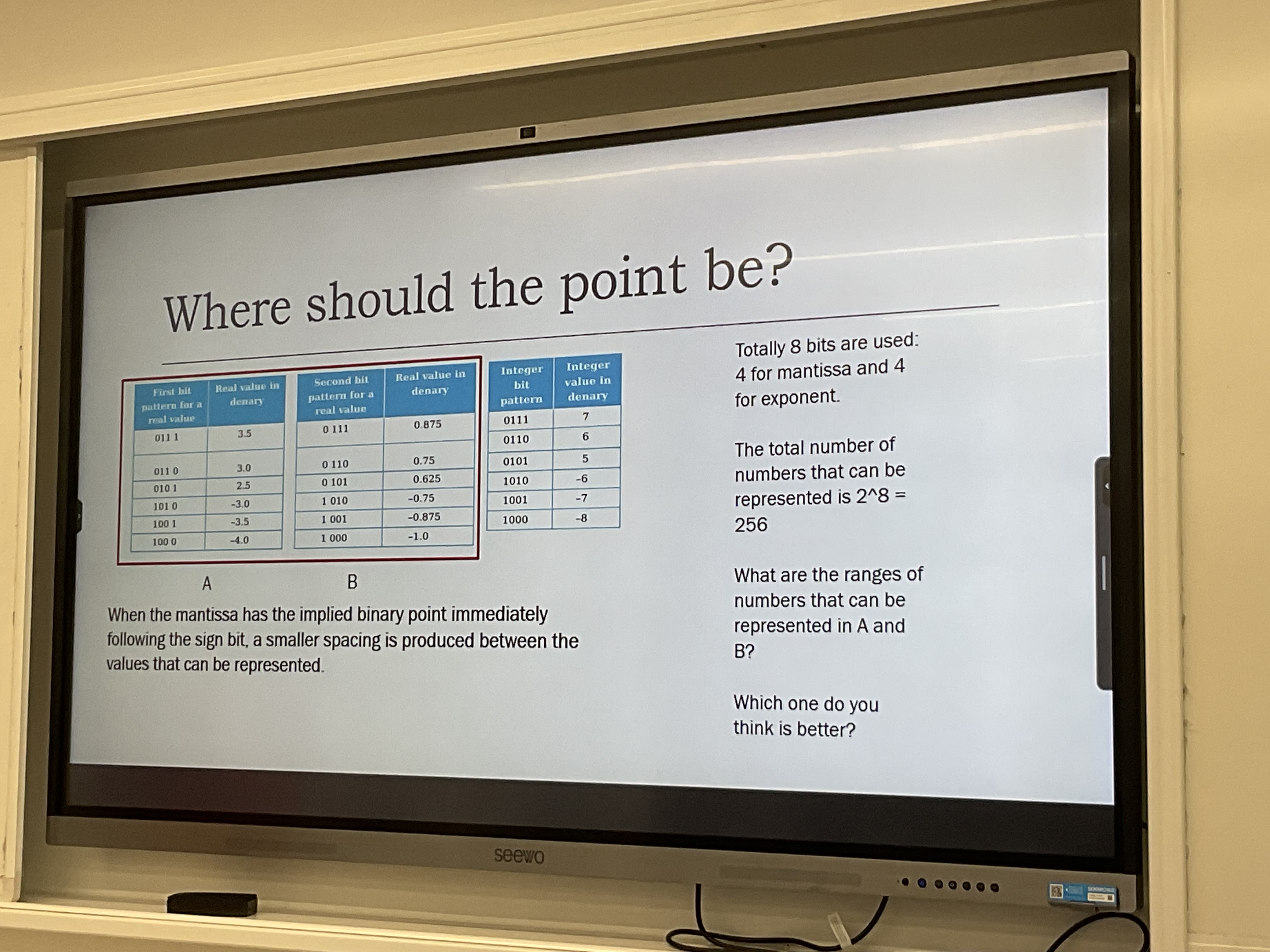
Where should the point be?

When the mantissa has the implied binary point immediately following the sign bit, a smaller spacing is produced between the values that can be represented.

• Example: Totally 8 bits are used: 4 for mantissa and 4 for exponent. The total number of numbers that can be represented is 2^8 = 256

Normalization:

What if 8 bits are used, 4 for mantissa, 4 for exponent?
Normalization is to achieve maximum precision by using all the bits fully.
Normalization:

For a positive number, the bits in the mantissa are shifted left until the most significant bits are 0 followed by 1.
For a negative number, the bits in the mantissa are shifted left until the most significant bits are 1 followed by 0.

Move to normalize form: 左侧不能出现连续的0。可将整体移位：

1. 小数点向右移动n位

2. 在小数点后exponential 部分binary number 减去n

Conversion of representations

2 → 10:

• Normalized floating-point number. 0100011 0100

• Mantissa: 0100011 →2425+26

• Exponent 0100 →4

• (242+25)X2 = 2+2+22=8.75

10 → 2

• Positive: 8.75

• 8 → 01000, remember to add an 0.

• 75 7 11

• 8.75 → 01000.11

• 8.75 → 0.100011 0100

• 8.75 → 0100011000 0100

yellow 10 bits for mantissa and 4 bits for exponent

Conversion of repersentations

• 有些小数永远无法被精确表示

  Let's consider the conversion of 8.63. The first step is the same but now the .63 has to be converted by the multiply by two and record whole number parts' method. This works as follows:
  .63 x 2 = 1.26 so 1 is stored to give the fraction .1
  .26 × 2 = 52 so 0 is stored to give the fraction .10
  .52 x 2 = 1.04 so 1 is stored to give the fraction .101
  .04 x 2 = 08 so 0 is stored to give the fraction .1010
  At this stage it can be seen that, multiplying .08 by 2 successively is going to give a lot of zeros in the binary fraction before another 1 is added so the process can be stopped. .63 has been approximated as .625. So, following Steps 3-5 in Example 1, the final representation becomes 0100010100 for the mantissa and 0100 for the exponent.
  

Problems with using floating-point numbers

Most decimal fractions cannot be represented exactly as binary fractions, i.e., floating-point numbers are just approximation of decimal fractions.

• Rounding error:
  • Increasing the number of bits used for mantissa
  

• Overflow and underflow

1. Overflow is a condition that occurs when an calculation produces a result that is greater than what given number of bits can store or represent

2. Underflow is a condition that occurs when a calculation produces a result that is less than what given number of bits can stored or represent.